E=mc^2 Explained
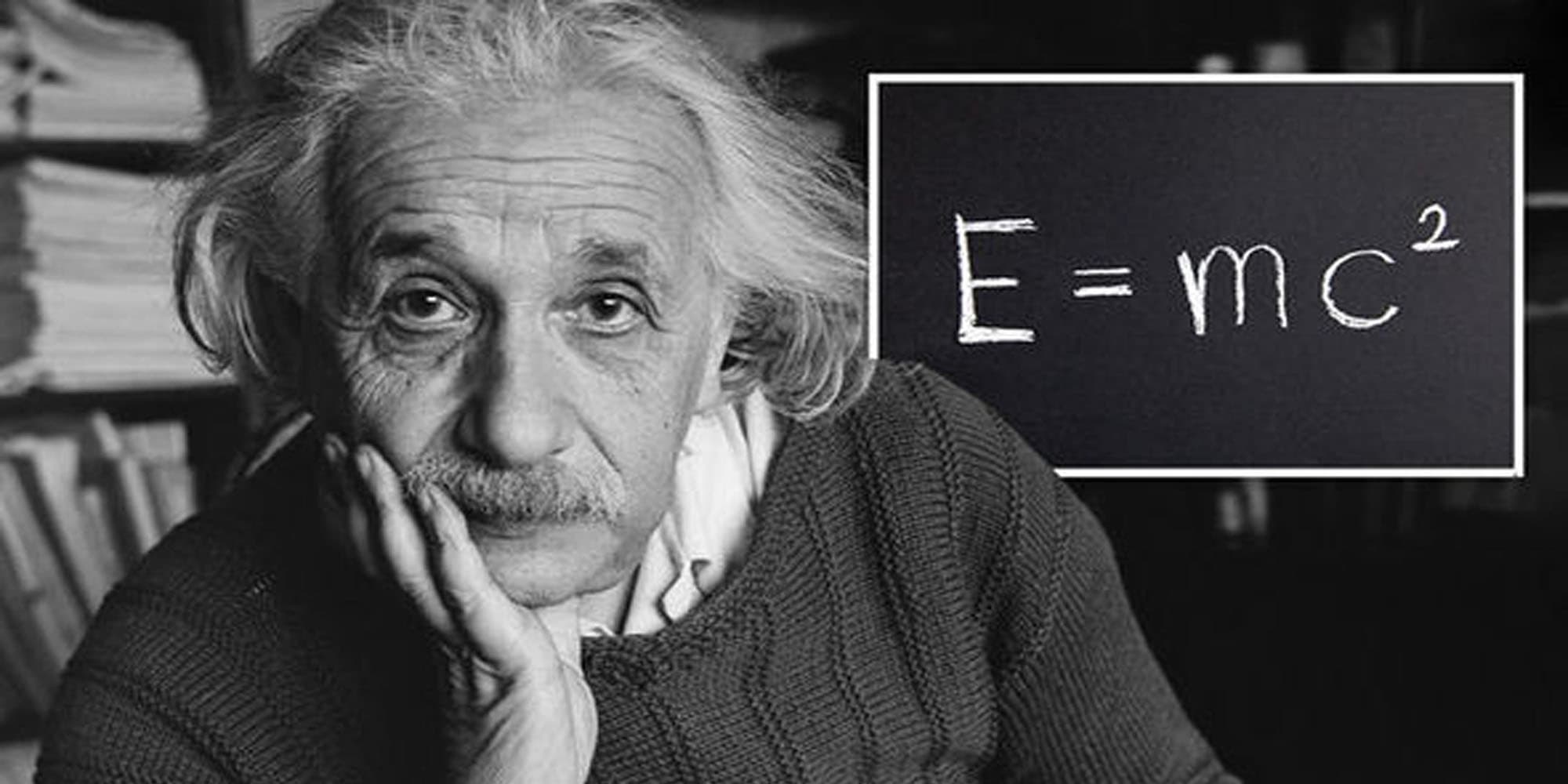
E=mc^2 explained
In 1905, Albert Einstein presented a groundbreaking idea to the scientific world: energy (E) and mass (m) are interchangeable. They are both different manifestations of the same thing and can convert into each other.
This concept was quite revolutionary at that time.
Described in the world's most famous equation: (E=mc^2), it changed the way we view the Universe.
What does (E=mc^2) really mean?
Energy (E) is equal to mass (m) times the speed of light in vacuum (c) squared.
But how is speed of light relevant in the relationship between energy and mass?
Why speed of light (c)?
It seems that the speed of light isn't just about light. It’s a fundamental constant in the laws of physics that govern our universe.
In fact, it's part of the very fabric of spacetime itself.
The speed of light in a vacuum is invariant – it remains the same for all observers, regardless of the motion of the light source or the observer.
It is a universal physical constant that is exactly equal to 299,792,458 metres per second (m/s).
That’s speed!
In essence, this is why the speed of light appears in the equation; not because light has something specifically to do with mass or energy.
Or maybe it appears because it’s the port to another universe, or another space, or another time, or no time, where the motion of the light source and the observer are immaterial or irrelevant.
If Many-worlds interpretation (MWI) is possible, why not?
But I won’t go into that now…
Why squared (^2)?
The answer comes from the mathematical structure of spacetime in Einstein's theory of special relativity. In this framework, we see the speed of light squared appearing naturally in the core geometry of spacetime.
In other words, it usually somehow works.
Why speed of light squared (c^2)?
The term c^2 serves a specific role: it's a conversion factor. It's there to ensure the units on both sides of the equation match up.
It allows us to convert between the units of energy (joules) and mass (kilograms), making the interchangeability of mass and energy not just a theoretical concept, but one that can be applied in practice.
E=mc^2 in practice
This relationship has been tested and confirmed in numerous experiments and observations, which have shown that E=mc^2 accurately describes how mass and energy are related in a wide variety of situations.
Some interesting examples:
i. Nuclear reactions
Both nuclear fission (splitting a larger nucleus into smaller ones, as in a nuclear power plant) and nuclear fusion (combining small nuclei into a larger one, as in the Sun or a hydrogen bomb) convert a small amount of mass into energy.
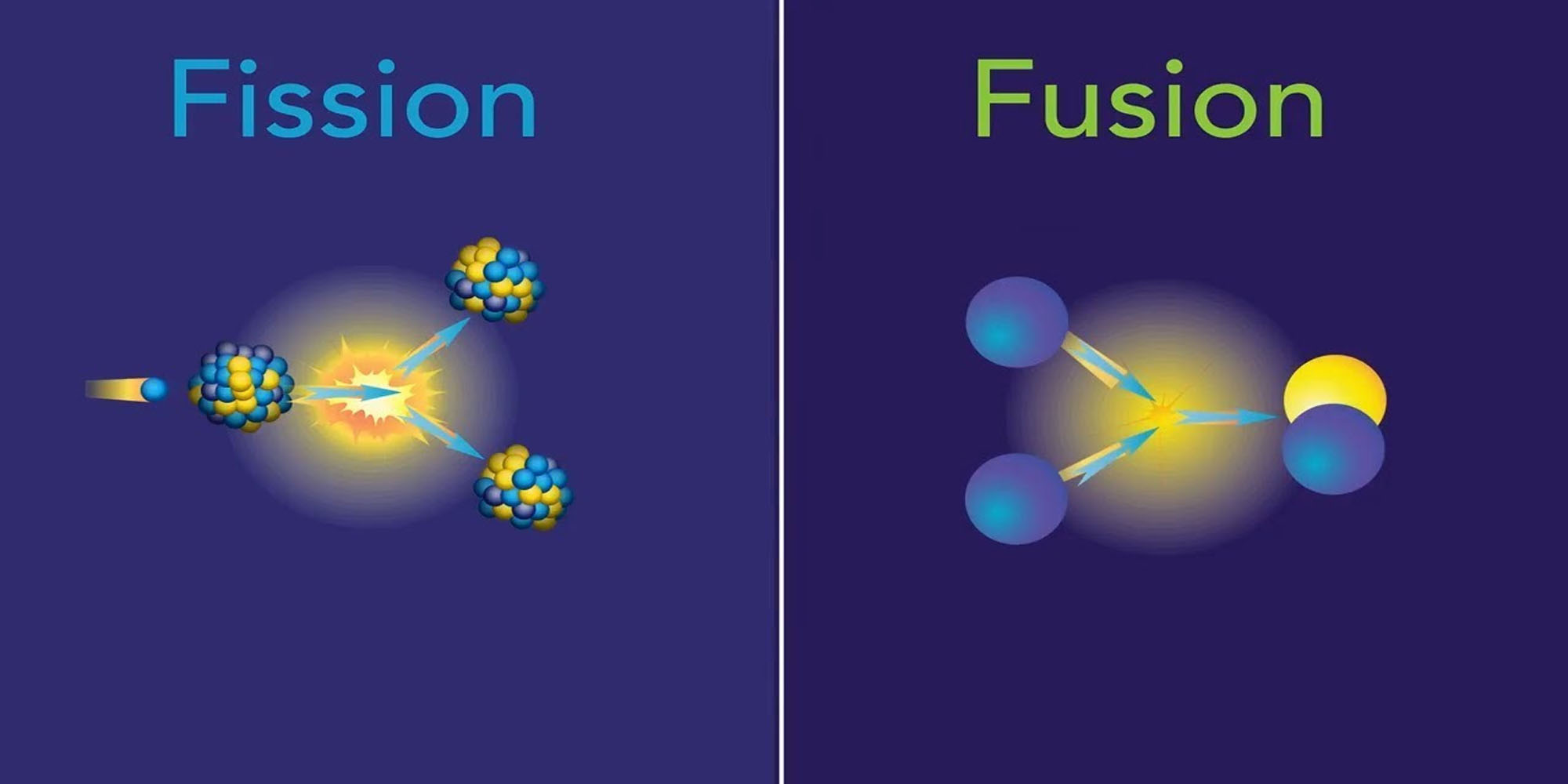
If we measure the masses of the particles before and after the reaction, we’ll find that some mass is lost.
If we measure the energy produced, for instance by the heat generated, we’ll find that the lost mass times c^2 equals the energy produced.
One of the first tests to indirectly confirm E=mc^2 was in the 1930s, when the physicist Enrico Fermi conducted experiments that involved bombarding various elements with neutrons, which showed that nuclear reactions resulted in the release of a significant amount of energy.
However, the mass before and after the reaction was not measured during the experiments, to confirm E=mc^2 directly.
Those days, with no measurements or audit trails.

Validation would come later with other experiments in nuclear physics and particle physics.
ii. Astrophysics

When we look at the light emitted by stars, we are witnessing the conversion of mass into energy.
Stars generate energy by nuclear fusion: the cores of stars under high pressure and temperature convert hydrogen into helium.
The mass of the helium atom produced is less than the mass of the four hydrogen atoms that went into making it.
This "missing" mass has been converted into energy, which is radiated away in the form of light and other particles.
Of course, there is no direct way to measure this with absolute precision. In this case, the equation is validated through astrophysical observations.
Stellar models, which account for the energy produced through fusion and the observed brightness and spectra of stars, align well with the predictions of E=mc^2.
iii. Particle accelerators

Particle accelerators, like the Large Hadron Collider (LHC), use pulsed electromagnetic fields to accelerate charged particles up to 99.99999896% the speed of light.
At these speeds, the particles can be smashed together to produce collisions with immense amounts of kinetic energy.
When particles collide at such high speeds in accelerators, the total energy of the colliding particles (which includes their kinetic energy and their rest energy, represented by their mass) becomes available for the production of new particles.
The motion (kinetic energy) and the inherent energy of the particles' mass contribute to the formation of new particles.
Conversely, when certain particles decay or combine post-collision, they can release energy.
When measured, the difference in mass between the original particles and the decay products, times c^2, equals the energy released.
The total energy before the collision (mostly kinetic energy of the moving particles) is conserved and equals the total energy after the collision (a combination of kinetic energy, rest energy of new particles, and any radiated energy), demonstrating E=mc^2.
One of the first indirect confirmations of E=mc^2 came in August 1932.
Using a cloud chamber to examine the tracks left by cosmic rays (as one usually does on a Monday morning), Carl Anderson accidentally discovered “a particle with a positive charge but with a mass seemingly equal to that of an electron”.
This particle, named the "positron," was the first antiparticle proven by experiment.
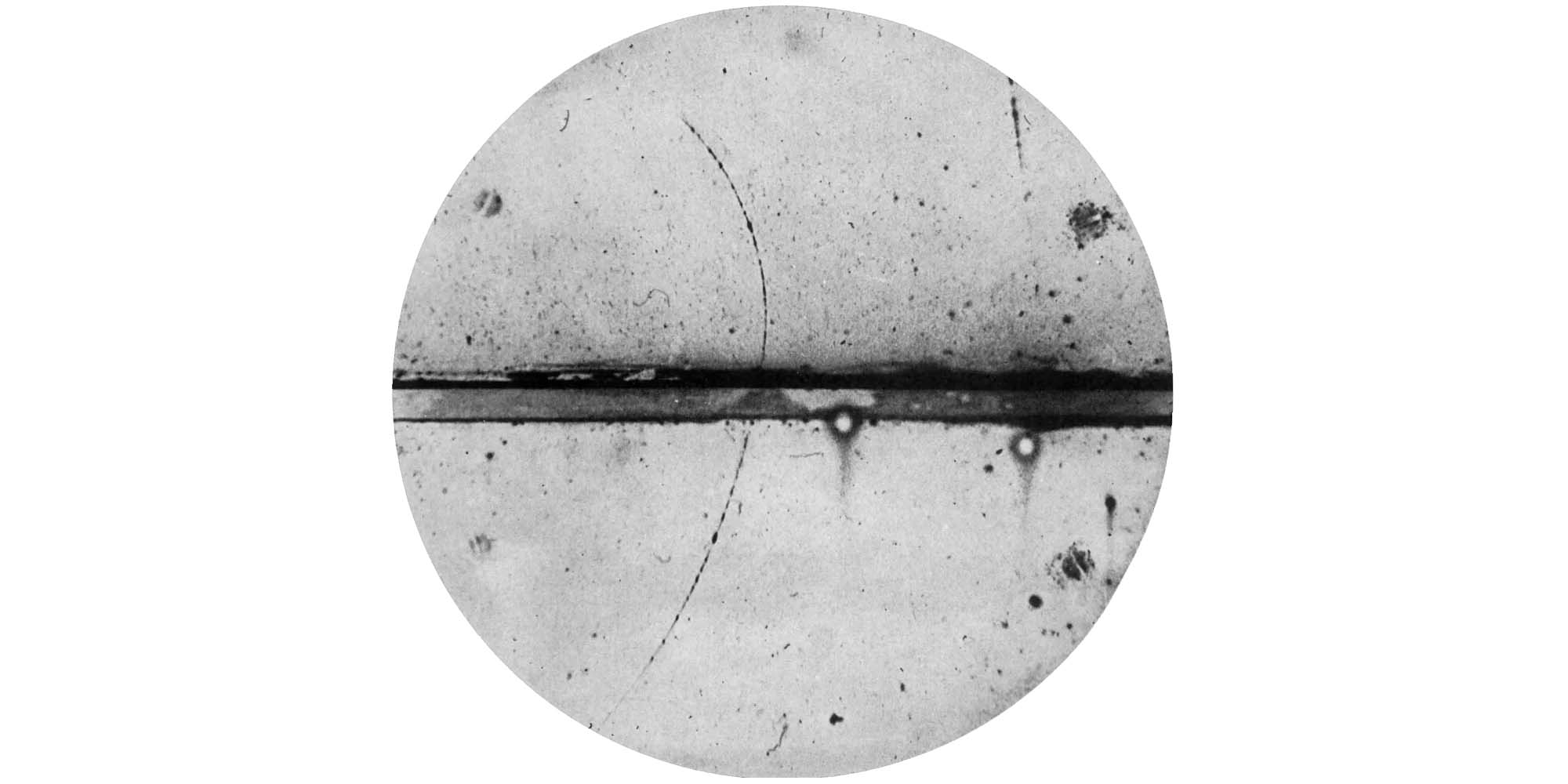
What a great accident! Thinking of my accidents… not that great!
This discovery was significant for E=mc^2.
It provided experimental evidence that high-energy particles from cosmic rays, when interacting with matter, could produce secondary particles, including gamma rays.
When these gamma rays have sufficient energy and interact with the nuclei of atoms, they can lead to the production of particle-antiparticle pairs (such as electron-positron pair).
The energy of the gamma ray that’s converted into pairs corresponds to the combined rest mass of the particles produced.
Unfortunately, as with Fermi's experiment mentioned before, the direct measurement of energy and mass before and after the collisions was not done.
Yes, those days.

This level of precision would come later with more advanced particle accelerators and detection equipment.
iv. Precise Mass Measurements in Atomic Reactions
The most direct and high precision test of E=mc^2 was performed in 2005, by a team led by physicist David E. Pritchard at MIT, using a Penning trap mass spectrometer.

They accurately measured the masses of individual particles: a neutron, a helium-4 ion, and a Silicon-28 ion.
The focus was on the energy released when helium and a neutron combine to form silicon.
In such nuclear reactions, some mass is typically lost.
The team found that the "lost" mass, when converted into energy using E=mc^2, matched exactly with the energy released, thus confirming Einstein's equation in the context of nuclear reactions.
E=mc^2 bonus
Did you know that (E=m)?
The electron-volt (eV) is the amount of kinetic energy gained or lost by a single electron accelerating from rest through an electric potential difference of one volt in vacuum.
If we measure mass in units of eV/c^2 (electron-volts divided by the speed of light squared), and we measure energy in eV (electron-volts), then the equation simplifies to E=m.
Because E=mc^2 would become eV=eV/c^2*c^2.
And *c^2 and /c^2 would cancel each other.
Therefore, eV=eV, which in this case means E=m.
To be clear, this doesn't mean that mass and energy are "the same thing".
It just means that they are equivalent in the sense that mass can be converted into energy and vice versa, and that this conversion factor is the speed of light squared.
Ok, so, now that I explained E=mc^2 (well, I tried), let’s continue...