God Does Not Play Dice with the Universe
Cover Image by: Public domain via Wikimedia Commons
Can the universe be governed just by probabilities?
According to Einstein, no. As he famously stated:
“God does not play dice with the universe".
Are you wondering how come he said that?
Well, this is an interesting story!
It starts almost 100 years ago…
During 1925, a new theory was formed.
The Copenhagen Interpretation
The collection of theories and rules that govern quantum mechanics.
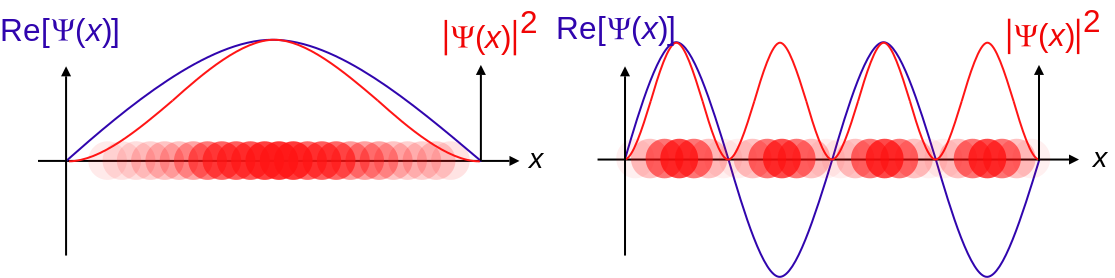Wavefunctions – public domain from Wikimedia Commons
Due to the nature of these rules, it was proposed that quantum mechanics is intrinsically indeterministic.
So, the quantum world is inherently unpredictable!
We can only determine the probability of finding a result.
Even if we have all possible information about a given system.
_Surface_Plot.jpg)
2D wavefunction – Inductiveload, Public domain, via Wikimedia Commons
To give you some context, I’ll (try to) explain the rules - in a nutshell:
Quantum Superposition and Wave Function Collapse
Interference electrons – Alexandre Gondran, CC BY-SA 4.0 via Wikimedia Commons
A particle (e.g., electron) can exist in multiple states at the same time (superposition) until observed. So:
-
Before measurement, the wave function is in superposition of all possible states (e.g., spin-up and spin-down).
-
Upon measurement, the wave function collapses, and the particle is observed in just one of the possible states (e.g., either spin-up or spin-down).
This collapse is inherently random, so the exact outcome cannot be predicted with certainty before observation.
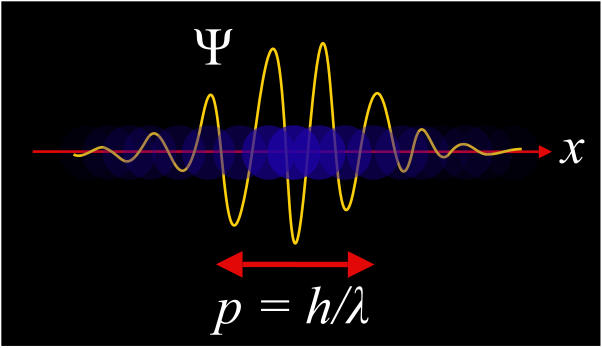Wave particle duality – Maschen, CC0, via Wikimedia Commons
Can you imagine how it is to be everywhere at the same time? Not here or there, but in all possible locations at once. That’s how I think of superposition.
I try to imagine it. It’s fun!
Now, can you imagine how it is to collapse from that superposition, lose your free will, and have a distant third-party observer determine your path?
That’s how I imagine the wave function collapse upon measurement!
Not so fun.
The Born rule
The probabilities of the different possible outcomes are calculated using the Born rule.
This rule was formulated by Max Born in July 1926.
Max Born – Public domain from Wikimedia Commons
The Born rule is a formula. A tool to calculate the probability of finding a given result upon measurement.
With the Born rule, we predict the likelihood of finding a system (e.g., electron) in a given state (e.g., spin-up).
Considering that:
-
The wave function is where all information about a quantum system is described.
-
For a single particle, like an electron, the wave function can give information about its possible position, momentum, spin, and other quantum properties.
The information is extracted from the wavefunction using the Born rule, to predict the probability of observing a specific state (e.g., spin-up) of the quantum object (e.g., electron).
Easy!
The Uncertainty Principle
This principle was formulated by Werner Heisenberg in March 1927.
Werner Heisenberg – Public domain on Wikimedia commons
It provides a restriction (numerical boundary) on the precision with which certain pairs of complementary properties (such as position and momentum) can be simultaneously known.
The Principle of Complementarity
Niels Bohr publicly introduced the principle of complementarity in September 1927.
Niels Bohr – photograph by public domain on Wikimedia commons
Bohr's idea was that certain pairs of properties, like position and momentum or energy and time, are complementary in the sense that they cannot be precisely measured or known simultaneously.
If one property is measured with high precision, the complementary property becomes inherently uncertain.
Initially, I thought this means “the more you know, the less you know”. But I am starting to think that this might mean “the less you know, the more you know”.
Anyway.
So, these are the rules of the Copenhagen Interpretation - in a nutshell.
Einstein’s Views
.png)
Albert Einstein - Photograph by public domain on Wikimedia commons
Fundamental Probabilities
Einstein was not satisfied with the probabilistic nature of the interpretation.
As he stated in his Letter to Max Born in December 1926:
“Quantum mechanics is certainly imposing. But an inner voice tells me that it is not yet the real thing. […] I, at any rate, am convinced that He does not throw dice.”
Fundamental Indeterminism
Physicist such as Niels Bohr, Werner Heisenberg and Max Born, among others, proposed that the indeterministic nature of the theory was fundamental to it.
As they explained, unlike classical mechanics, in the quantum world there is no underlying deterministic order to be found.
This is not a concept you can easily accept if you know classical mechanics.
Table of Mechanicks – The drawing is signed 'Fletcher Sculp', Public domain, via Wikimedia Commons
And you know classical mechanics just by observing the world around you.
In a deterministic system, the future state or behavior of an object is entirely determined by its initial conditions and the rules governing its evolution.
There's no randomness or unpredictability involved.
If you decide to throw a ball, and you know its initial properties (such as position, velocity, gravity), then you can determine its future position and velocity, with complete accuracy.
So, it's normal to find quantum theory a bit “shocking” – it’s different to everything we know!
Exploring Deep Galaxy – Image by stockgiu on Freepik
As Niels Bohr stated:
"If quantum mechanics hasn't profoundly shocked you, you haven't understood it yet."
I surely don’t understand it. Yet I am still profoundly shocked.
Imagine how Einstein felt when he was told that outcomes could only be calculated based on probabilities, and that the more we know about some properties the less we know about others.
.jpg)
Albert Einstein 3 years old - Public domain via Wikimedia Commons
This did not make sense.
And, for Einstein, physics must make sense!
If we had all information, we would be able to calculate all properties of particles with certainty.
In his view, we simply did not have all information.
So, in October 1927, he shared his views with the scientific community.
Fifth Solvay Conference 1927
Solvay conference 1927 by public domain on Wikimedia commons
Even though the conference in Brussels was planned for discussions around the electron and photon, Copenhagen Interpretation was the main subject under dispute.
Imagine that room.
The world's most notable physicists coming together to discuss the future.
29 attendees – more than half of them being Nobel Prize winners!
Debating and discussing the rules of quantum mechanics. Giving birth to all ideas that govern the technology we use today!
Thought Experiments During Conference
Einstein presented several thought experiments during the conference, to challenge the Copenhagen interpretation.
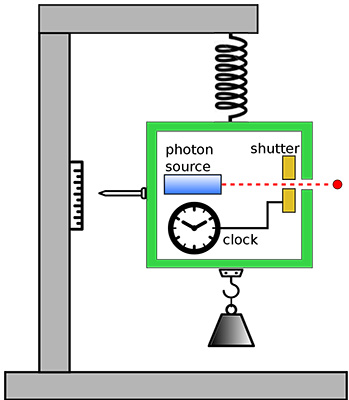Einstein's Light Box – Prokaryotic Caspase Homolog, CC BY-SA 4.0 via Wikimedia Commons
These were aimed at highlighting what he perceived as inconsistencies in the interpretation, particularly with respect to the role of measurement and the concept of wave function collapse.
Einstein believed that there must be some "hidden variables" that determined the outcomes. And that the measurements simply revealed those predetermined outcomes.
Philosophical Debate
"Einstein, stop telling God what to do", said Bohr to Einstein.
Einstein and Bohr - Photograph by public domain on Wikimedia commons
The conference witnessed a deep philosophical debate between the two.
Einstein's thought experiments were aimed at showing that the Copenhagen interpretation leads to paradoxes and inconsistencies, while Bohr defended the interpretation by showing that it remains internally consistent even when faced with these challenges.
The broader community was generally more aligned with Bohr's views, accepting the Copenhagen interpretation as a valid description.
Einstein’s Pursuit of a Complete Interpretation
Einstein Photo – Unknown photographer, Public domain, via Wikimedia Commons
Following the discussions and debates at the conference, Einstein continued to explore his concerns about the Copenhagen interpretation.
This pursuit eventually led to the formulation of a thought experiment, that aimed to demonstrate that quantum mechanics, as it was understood at the time, was incomplete.
To develop this concept further, Einstein collaborated with two other physicists, Boris Podolsky and Nathan Rosen.
The EPR Paper
In 1935, Albert Einstein, Boris Podolsky, and Nathan Rosen, published a paper titled "Can quantum-mechanical description of physical reality be considered complete?".
Media presented this as an “attack to quantum theory”.
NYT May 4, 1935 – New York Times, Public domain, via Wikimedia Commons
It was not.
This was merely an effort to further understand the newly formed theory. An attempt to collectively discover any missing elements, to ensure that the theory corresponds to the objective reality we experience.
And it worked!
This collaboration allowed them to present a strong argument questioning the completeness of quantum mechanics.
It was the beginning of research and experimentation, that lasted almost a century!
The paper is commonly known as the Einstein-Podolsky-Rosen (EPR) paper.
However, it is said that EPR refers to “Elements of the Physical Reality”.
In fact, we see this reference in the first page of the mentioned paper (See marked in the picture below).
The EPR Paradox
In the EPR paper they presented a thought experiment, to illustrate a paradox in the context of quantum mechanics.
The experiment considered the following.
Two particles, A and B, are prepared in a way that their position and momentum are correlated.
They are then spatially separated - moved to two different places.
In accordance with the proposed quantum theory:
-
Neither particle has a definite position or momentum until measured. The position and momentum are unknown before observation.
-
When the position of particle A is measured, its wave function collapses, and its position is determined.
-
The measurement on particle A has an instantaneous effect on the state of particle B, no matter how far apart they are (the “spooky action at a distance” we now call entanglement).
-
The effect is that the wave function of particle B collapses simultaneously with particle A, determining the position of particle B as well, even though no measurement has been performed on it yet.
-
The same would happen when measuring the momentum of Particle A.
However, an object is only directly influenced by its immediate surroundings (principle of locality).
So, particle A cannot directly influence particle B while they are far apart.
Therefore, if the results are indeed perfectly collated, there must be some other explanation for this phenomenon.
An element we are unaware of, causing what we observe.
EPR Argument
“In a complete theory, there is an element corresponding to each element of reality. […] If, without disturbing a system, we can predict with certainty the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.”
The EPR paper posed the question of completeness, implying that if the position or momentum of a particle (“physical quantity”) is perfectly correlated with the position or momentum of another particle, which is spatially separated, then there must be an “element of physical reality corresponding” to this position or momentum.
In other words, there may be a missing element, some “hidden variables”, not described in the proposed theory, which determine the position and momentum of both particles.
In their view, measurement reveals predetermined results. It does not create them. And particles don’t assign properties to other distant particles because they are being measured. Particles already have determined states before measurement. We just don’t know how these are defined.
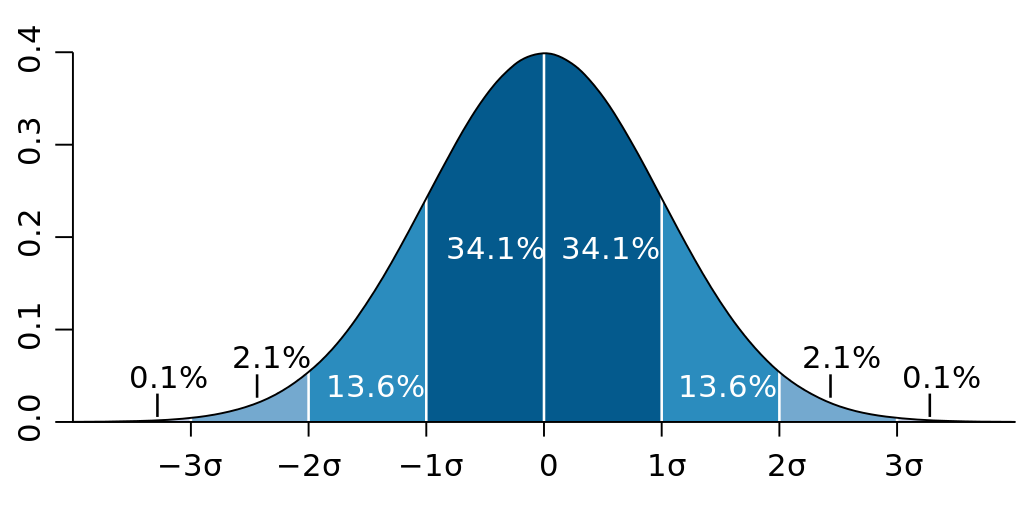Standard Deviation Diagram – M. W. Toews, CC BY 2.5 via Wikimedia Commons
EPR Conclusion
As a result, they concluded that:
“the quantum-mechanical description of physical reality given by wave functions is not complete."
Albert Einstein photo 1921 – Underwood and Underwood, New York, Public domain via Wikimedia Commons
They stated:
"While we have thus shown that the wave function does not provide a complete description of the physical reality, we left open the question of whether or not such a description exists. We believe, however, that such a theory is possible."
What Happened After the EPR Paper?
Niels Bohr and Albert Einstein – Paul Ehrenfest, Public domain, via Wikimedia Commons
The publication of the EPR paper sparked intense debates and further investigations into the foundations of quantum mechanics.
This led to the formulation of new theories and interpretations.
The power of collaboration and knowledge sharing!
"On the Einstein Podolsky Rosen Paradox"
In 1964, John Bell addressed the EPR paradox, and the question of whether "hidden variables" could explain the “spooky” quantum correlations observed.
John Bell – CERN, CC BY 4.0 via Wikimedia Commons
Bell formulated what is now known as the Bell's theorem, which challenged the notion of "local hidden variables" proposed.
Bell's Inequalities
In this theorem, Bell developed a mathematical inequality (Bell's inequality) that must be satisfied by any theory which is based on local hidden variables.
This inequality was a way to test the validity of these local hidden variable theories against the predictions of quantum mechanics.
Bell's test
Two correlated particles are spatially separated, possibly at a great distance from each other.
The experiment involves measuring certain properties of these particles (e.g., spin) using two separate detectors with adjustable settings.
-
If the universe is 'local' and the properties of particles are predetermined, then the statistical correlations between measurements of these properties, at two distant locations, should adhere to specific bounds defined by the inequality (Bell's inequality).
-
If experimental results show violations of these bounds, this should imply that the behaviour of particles cannot be explained by any local hidden variable theory, supporting the quantum mechanical description.
The bounds mentioned here are numerical boundaries derived from the statistical predictions of local hidden variable theories.
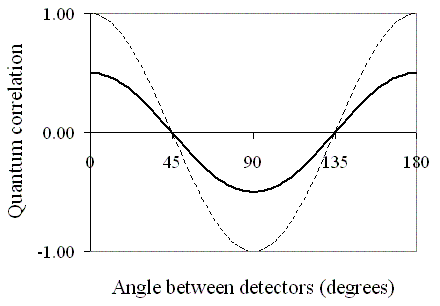Quantum Correlation - Caroline Thompson, CC BY-SA 3.0 via Wikimedia Commons
In other words, there is a threshold value (upper limit) that the correlations between measurements should not exceed if the world is classical and local.
If quantum experiments show correlations that exceed this threshold, this would indicate that quantum mechanics is a more accurate description of the physical world, by allowing non-local interactions.
John Bell Commenting – CERN, CC BY 4.0 via Wikimedia Commons
Violation of Bell's Inequalities
Following Bell’s publication, various experiments were designed by physicists, to test the fundamental nature of quantum mechanics.
Such as:
- Stuart Freedman and John Clauser experiment in 1972, which showed violations of the inequalities, supporting quantum mechanics over local hidden variable theories.
Stuart Freedman and John Clauser Experiment - Via Berkeley University
- Alain Aspect's experiments in 1982, which provided stronger evidence for the violation of Bell's inequalities, confirming the predictions of quantum mechanics regarding non-local correlations.
Alain Aspect's Experiment - Via Nobelprize.org
Vulnerable Experiments
But the experiments conducted in the 1970s and 1980s were vulnerable to certain loopholes.
In other words, something else could have caused the observed results.
The most prevalent loopholes:
- the locality loophole: one particle may influence the other particle within the time frame of the experiment, undermining the assumption of locality.
If information could be exchanged between the particles during the measurement process, the observed correlations might be attributed to this communication, rather than the non-local correlations predicted by quantum mechanics.
- fair sampling loophole: the subset of particles that are successfully detected and measured, may not accurately represent the entire group of particles.
Not all particles that are emitted are detected. Some are lost during transmission, especially over long distances. If the detectors are “biased” in such a way, this could potentially lead to misleading results.
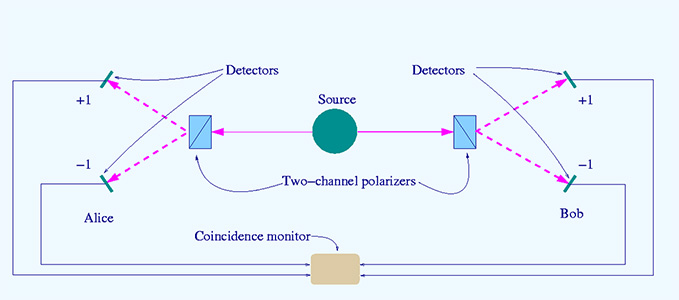Bell test photon analyer – By Maksim wikimedia commons
Loophole-Free Experiments
Three independent groups, in three different countries, published the most significant Bell tests, within three months, all in 2015!
They all supported the idea that objects separated by great distance can instantaneously affect each other’s behaviour.
And this time – the said experiments were “loophole-free”.
“Spooky action at a distance” confirmed!
Confirmed with “spooky action” by these distant, yet so connected, teams:
- Delft Experiment, by a team at the Delft University of Technology in Netherlands.
- Vienna Experiment, by a team at the University of Vienna in Austria.
- Boulder Experiment, by researchers at the National Institute of Standards and Technology in Colorado (NIST).
In addition to the locality loophole and fair sampling loophole, the teams also addressed:
- the memory loophole: the outcomes of measurements could be influenced by the memory of past settings and results, potentially leading to false violations of the Bell inequalities.
Most experiments have repeated measurements at the same two locations. Local hidden variable theory may exploit memory of past measurement settings and results. This could affect the outcomes and wrongly show a violation of the Bell inequality.
Experiments Are Ongoing
In May 2023, a group at ETH Zurich, confirmed even further the theory of quantum mechanics, this time using superconducting circuits to perform the experiment.
Fancy!
The end.
Is it the end?
Never in the quantum world!
While the Copenhagen interpretation is accepted as the cornerstone of modern quantum physics, the journey is not over.
New experiments may lead to new discoveries that may change our views of the universe.
But even if the theory of quantum remains as is, there are so many more mysteries yet to be uncovered.
As Sean Carroll (theoretical physicist) said:
“even if it’s right, it doesn’t mean we’re done - it doesn’t say that we’re anywhere close to figuring out a theory of everything”.
“The only thing I know, is that I know nothing.” – Socrates